In this post I show how helpful trigonometry can be when it comes to catching rabbits.

Problem

Alice just spotted a white rabbit urging to its rabbit hole ! Given the coordinates of the positions A, B, H, of Alice, the rabbit and the hole, as well as the respective speeds $S_A$ and $S_B$ of Alice and the rabbit, say whether Alice can catch the rabbit before it disappears, and give the time and place of the fastest possible interception.

Solution

I guess that I am not the first one to solve this but I couldn’t find any simple solution on the internet. The one I am giving here relies on trigonometry, but interestingly it doesn’t require to compute any trigonometrical function !

If sines give you fever, don’t wait for the first sines of fever (uh uh uh), just skip this part, I summarize everything in the next section.

We call C and $t_C$ the location and the time of the catch. It is straightforward that, since we are looking for the fastest catch, Alice’s trajectory towards C must be a straight line. Here is a sketch of the problem:

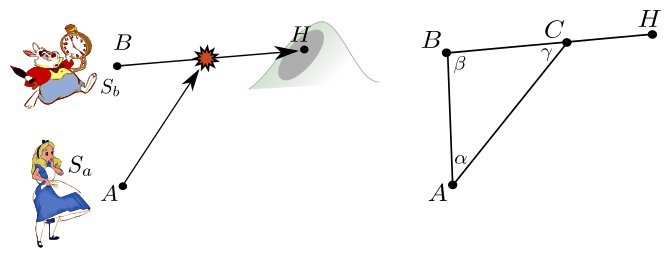Note that the lengths AC and BC denote the distance run by Alice and the Rabbit until the catch, therefore they verify

So finding the length BC would answer the problem, as it would tell us whether Alice can catch the rabbit before it reaches the rabbit hole (case $BC<BH$), and would immediately lead to both the location and time of the catch :

To express BC using the coordinates of the points, let us apply the famous Law of Sines to the triangle ABC:

Wich leads to

Now all we have to do is to express $\sin \alpha$ and $\sin \gamma$ in function of the given data. To do so we first compute $\sin(\beta)$, then we express $\sin \alpha$ with $\sin \beta$, and we express $\sin \gamma$ as a function of $\sin \alpha$ and $\sin \beta$.

The value of $\sin \beta$ can be computed from the points coordinates as follows:

Then we use the Law of Sines again, to compute $\sin \alpha$:

This only makes sense, of course, if

If this is not the case we conclude that Alice will never catch the rabbit, which solves the problem.

Finally we use the fact that the angles of a triangle sum to $\pi$ to compute $\sin \gamma$:

We reformulate using the already-copmputed $\sin \alpha$ and $\sin \beta$:

And… we are done, we have everything we need to compute BC and answer the problem.

Summary and code

So here is the short answer to the problem:

• Compute $\sin \beta$ using the formula given above.
• Compute $\sin \alpha = (S_b * \sin \beta)/S_a$. If $\mid \sin \alpha \mid>1$, Alice cannot catch the rabbit. Otherwise, advance to step 3.
• Compute $\sin \gamma$ with the formula above and the values of $\sin \alpha$ and $\sin \beta$ found in steps 1 and 2.
• Compute BC using the formula given above and the values found for $\sin \alpha$ and $\sin \gamma$. If $BC>BH$, the rabbit will reach its hole before Alice can catch it. Otherwise, congratulation young girl, you will eat rabbit for dinner, here are the location and time of the fastest possible interception:

Below is a script implementing this technique using Python’s pylab module:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

from pylab import * # imports srqt, norm, array, plot...

def interception(A, B, H, Sa, Sb):
    """ Returns ``(t_C, C)`` if A can catch B, before B 
    reaches H. Otherwise, returns ``None``. """

    AB, AH, BH = norm(A-B), norm(A-H), norm(B-H)
    sin_b = det(array((A-B,H-B))) / (AB*BH)

    sin_a = (Sb / Sa) * sin_b

    if abs(sin_a) > 1 :

        print("B moves too fast to be ever caught !")
        return None

    else:

        sin_c = ( sin_a * sqrt(1 - sin_b**2)
                  + sin_b * sqrt(1 - sin_a**2) )

        BC = AB * (sin_a / sin_c)

        if BC > BH:

            print("B reaches H before interception by A !")
            return None

        else:

            print("A intercepted B !")
            t_C = BC / Sb
            C = B + BC * (H-B)/ BH
            return t_C, C

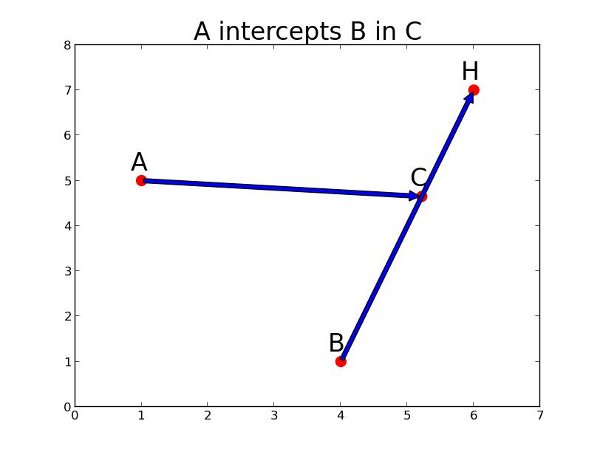
And here it is in action:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# PARAMETERS OF THE PROBLEM
A = array(( 1.0 , 5.0 )) # Alice's initial position
B = array(( 4.0 , 1.0 )) # Rabbit's initial position
H = array(( 6.0 , 7.0 )) # The hole's coordinates
Sa = 1.1 # Alice's speed
Sb = 1.0 # Rabbit's speed

# Find the intersection
t,C = interception(A, B, H, Sa, Sb)

# Plot the results

scatter(*zip(A,B,H,C), s=100, color='r')

for label, point in zip(['A','B','H','C'], [A,B,H,C]):
    annotate( label, xy = point, xytext = (-10, 10),
              textcoords = 'offset points', fontsize = 24)

annotate("", xy=H, xytext=B, xycoords='data',
         textcoords='data',size=20,
         arrowprops=dict(arrowstyle="simple",
                         connectionstyle="arc3"))

annotate("", xy=C, xytext=A, xycoords='data',
         textcoords='data',size=20,
         arrowprops=dict(arrowstyle="simple",
                         connectionstyle="arc3"))

title("A intercepts B in C", fontsize = 24)

show()